2005年 算数オリンピック ファイナル
こんにちは。
昨日の書評はいかがでしたでしょうか?
普段感想文や論評を書くことはないのでかなり手こずりましたが、今後もちょいちょいこういう記事を入れていこうと思います。文章力の向上に期待していてください・・・!
さて、本日は昨日の記事の最後に問題を乗せていたことにお気づきでしょうか?
え?気づかなかった。という人のために問題も再掲しておきます。
そして気づいていた皆様、お待たせしました。今回は解説付きです。
2005年の算数オリンピック ファイナルからの抜粋で、実際の問題とは少し改題してあります。チャレンジした人はわかると思いますが、かなりの難問だと思います。
【問題】難易度:★★★★★
図のような台形ABCDと台形EFGHの面積の比を求めてください。
ただし、AB=AD=EH、BC=EF=GHです。
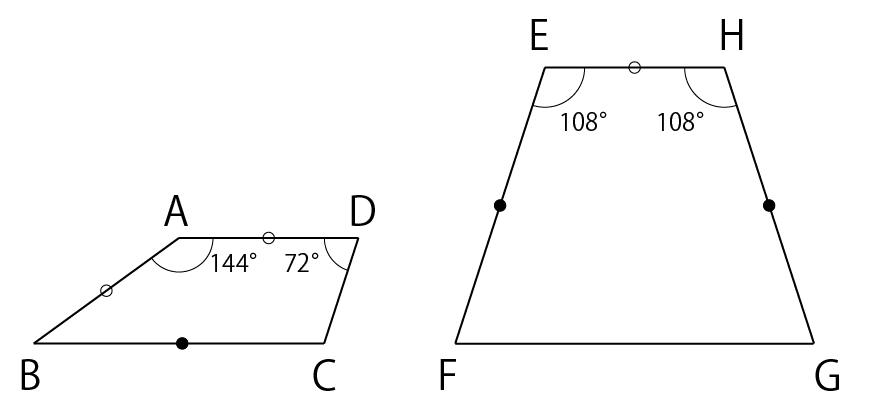
【解説】↓
解説に入る前に一言。
実際の問題では台形EFGHの面積が100㎠と与えられていて、台形ABCDの面積を求めるというものでした。面積が与えられると長さを求めたくなりますが、この問題の本質は2つの台形の面積比を求めるところにあります。そのため、あらかじめ問題設定を面積比を求めることに変えておきました。
今回はあえて正確な図を問題に提示しました。それを見よう見まねで描けば良いのですが、少し立ち止まってみましょう。この2つの台形のどちらが「この問題設定に支配的か」を考えてみましょう。基準とする長さはAB=AD=EHにします。(基準をBC=EF=GHにしても同じことです)
まず台形EFGHからみていきましょう。EHの長さを基準にして等脚台形を作ろうとすると、図のように様々な場合が考えられ、図形が定まりません。
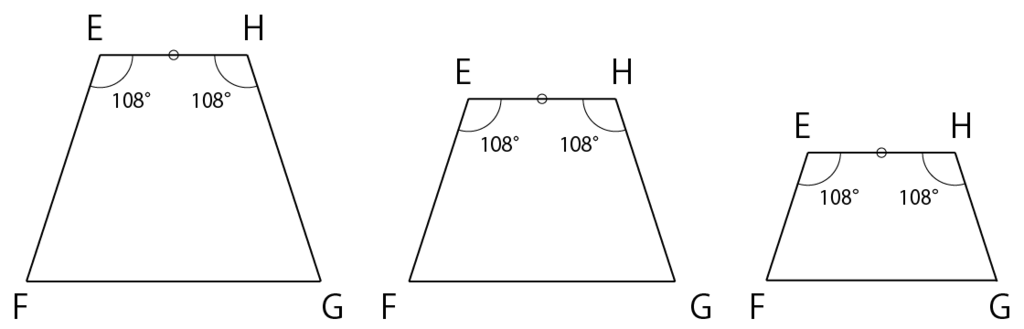
しかし、台形ABCDはどうでしょうか?下の図のように順番に描いていくと、現れる台形は1つに定まりますね。そして、定まったBCの長さを台形EFGHの脚にして仕舞えば良いわけです。

ということは、台形ABCDがこの問題設定を支配していることになります。言い換えれば、台形EFGHがBC=EF=GHによって補助されていると捉えられます。
2つの四角形は台形、つまり上底と下底が平行になっているので角度が全てわかります。残念ながらCDやFGに関してはこの時点では得られる情報がありません。
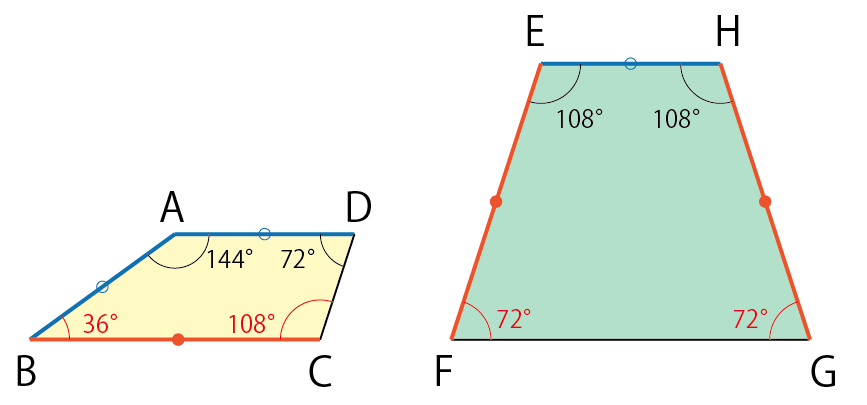
さて、このブログでも頻出のテクニック「足したり引いたりして有名角や等角を作る」というものがありますが、今回出てくる角度は全部36°の倍数です。そのため等角や有名角の作り方はめちゃくちゃたくさんあります。
ここでこの過去記事に想いを馳せてみましょう。
上の記事で使っている技は「図中の角度と正多角形を関連づける」というものでした。
今回の問題で使えるかわかりませんが、36°の倍数角は正五角形や正10角形と関連があります。このことも念頭に入れておきましょう。
以上のことを踏まえると、今回考慮すべき関連は
- 台形EFGHがBC=EF=GHによって補助されている
- 36°の倍数角は正五角形や正10角形と関連がある
- 36°の倍数角で作れる有名角といえば180°
になると思います。1つ目の関連は、等辺同士をくっつけるときはBCとEF(GH)をくっつけることを意味します。くっつけ方何通りかあるうち、下二つの関連をフルに使うためには下の図のように、正10角形を作ることがベストでしょう。(綺麗な図形ができるからここからたくさんヒントが得られる)。補足しておくと、」赤線の角度は全て144°です。
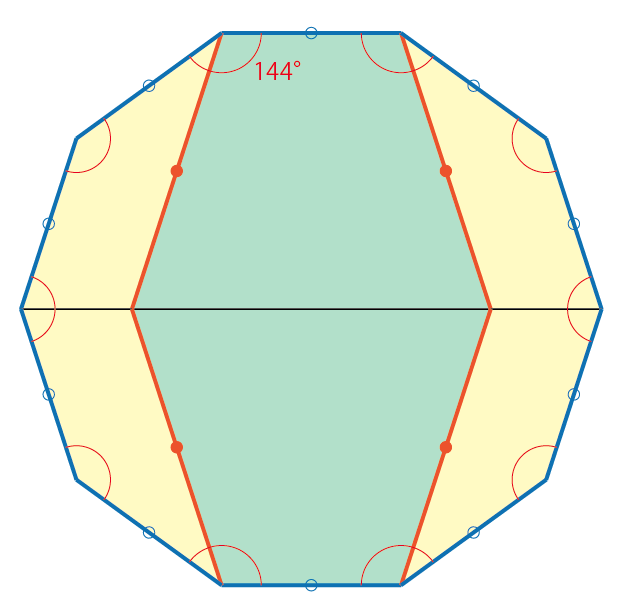
正多角形は中心を通る対角線によって合同な二等辺三角形の集まりと見做すことができます。
左の図のように台形ABCDに対して「い」、台形EFGHを中心を通る対角線によって分割してできる2等辺三角形に対して「あ」とします。
さらに、右の図において、正10角形は「あ」10個分に相当します。

正10角形の面積を考えると・・・
い×4+あ×6=あ×10 つまりあ=い
の関係が導けます。
以上から
(台形ABCDの面積):(台形EFGHの面積)=1:3
です。
【まとめ】
- 図形を決定する支配因子に着目する
- 正多角形には美味しい情報がたくさん隠れている
- とにかく有名角
- 正多角形には対角線をとりあえず引く
ではお疲れ様でした。そろそろまたオリジナル問題作ろうと思いますのでチャレンジしてみてください。