2001年 ジュニア算数オリンピック ファイナル
こんにちは。
最近は隙間時間にyoutubeに投稿しています。
昔は、詳細な解説をビッシリ描く事もできましたが、なかなか時間が取れず。
サクサクっと作れるyoutubeに切り替えています。。。
冒頭部分で問題紹介。
20秒くらいから解説という構成になっています。
ラストにはキーポイントを紹介しています。
是非ご覧になってみてください!
【挑戦者求ム!】 Jr.算数オリンピック 沼にハマる!?有名図形の面積を求める面白い難問!【レベル★★★★☆】
2001年 ジュニア算数オリンピック ファイナル 【解けそうで解けない!】
面積の難問をシンプルかつ分かりやすく解説!
シンプルな問題設定の、三角形の面積を求める問題。
シンプルな問題の方が難しい。算数・数学あるあるですね。
よく見かける角度がたくさん出てきますが・・・ うまく面積を求められる糸口を見つけられますか!?
是非チャレンジしてみてください。 別解もたくさんあると思います!
この解法の他に「おもしろい」「美しい」解き方を 発見した方は、コメントにて教えてください!
【レベル感】※独断と偏見です
☆☆☆☆★:難しい発想不要で、簡単に解ける
☆☆☆★★:中学入試の標準的なレベル
☆☆★★★:算数オリンピックの標準的なレベル(難関中学入試レベル)
☆★★★★:算数オリンピックの中でも比較的難問(灘中学レベル)
★★★★★:大人も苦戦する超難問。頭の柔らかさと引き出しの多さが問われます。
【生存報告】ご無沙汰しております
ご無沙汰しております。管理人です。
気づけば2年弱も放置していました。。。
この度、ここに載せている問題の解説を
YouTubeに移してみようかと思い立った次第で、
試しに一つアップしてみました。
【解けたら天才!?】算数オリンピック 2006年 ファイナルの超難問!
手書きの図で詳しくしゃべりながらやるのか、
鮮やかに解説する方がまとまりが良くて見やすいのか、
まだ分かりませんが、今回は後者の方でさらっと
テロップと既製の図のみで試しに作ってみました。
放置したにも関わらず、ありがたいことに
毎日そこそこのアクセス者がいらっしゃるので、
見にきていただけると嬉しいです。
チャンネル自体は「趣味の記録」みたいなものなので、
まとまりのない感じにはなってます。
以上、宣伝でした。
2012年 ジュニア算数オリンピック ファイナル
こんばんはお久しぶりです。1週間ぶりの更新です。
1週間ネタを仕込むことに専念しすぎて更新のことを完全に忘れていました。
どうやら予約投稿とかもできるらしいんでこれからは時間あるときに書き溜めて予約投稿機能使っていこうと思います。(情弱)
今まで長めの雑談の後に問題と解説を書くスタイルでしたが、分離させようと思います。雑談や書評などは同じブログ内で書くか、別のブログとして独立させるか悩みどころです。
しばらくは問題解説だけで行きます。
今回は2012年のジュニア大会の決勝問題。意味深な問題設定が特徴的な角度問題です。
条件が意味深すぎるので方針は立てやすいかも。。。?
【問題】難易度:★★★☆☆
下の図において、BD=DC、AD=AC、BF=DF+DGとなっているとき、角DCGの角度は?
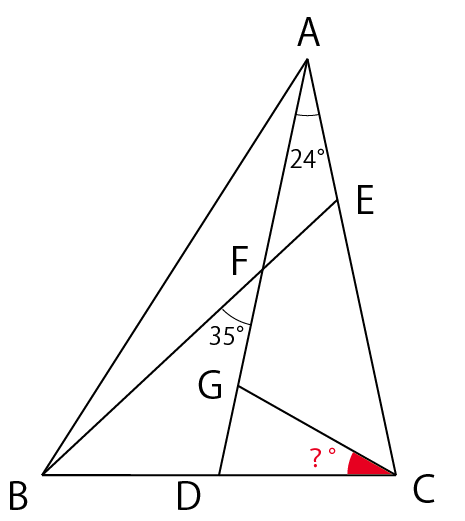
【解説】↓
二等辺三角形ACDを初めに描いて、BDを付け足すという手順で描けば作図はフリーハンドでもさほど難しくないでしょう。Gの位置が少し難しいですが、目算でBFとDFの差になりそうな位置を見つけましょう。
いつも通り等辺には印をつけて強調し、図がごちゃごちゃしない程度に角度を書き入れておきましょう。
ここで着目するべきは「BD=DCという条件からは角度の情報が引き出せない」ということです。次の段階でうまい操作によってこの条件が活きてくるはずです。現段階では?に対してめぼしい情報は得られません。

意味深な辺の長さの条件「BF=DF+DG」が今回の問題の鍵であることは皆さんもお分かりでしょう。こんなにあからさまに作為的な条件も珍しいものです。
これまで様々な問題で出てきた「分散した角度の条件は1箇所に集める」という手法と類似の手法を使用しましょう。
図形問題、特に角度問題では有名三角形や二等辺三角形が役に立つという経験則が染み付いていますから、この条件から「二等辺三角形が作れる」という発想に至ります。
さらに、前の段階で目をつけていたBD=DCもうまく使ってやりましょう。

上の図のように三角形BDFをくるっと回転させてBDとDCが重なるようにくっつけます。すると、「BF=DF+DG」によって三角形CGHは二等辺三角形となります。

すると、図のようにこの二等辺三角形の等角は72.5°とわかります。よって、三角形CDGに着目して、
?=29.5°
となります。
【まとめ】
- 分散している条件は1箇所に集める
- 等辺が出てきたらとりあえずくっつける
- 他の条件とコンビネーションで使えないか考える
小さな成功体験の積み重ね
こんばんは。
夜な夜なブログを更新中です。
最近になってありがたいことに「ブログ見てるよ」「いつも楽しみに待ってます」「今日こそは解きたい」「解説がわかりやすい」など、ブログ関連のことを話のネタにしてくれる人が増えてきました!
当ブログにご来訪くださっている皆さん本当にありがとうございます。とても励みになります。
こうやって声をかけてくれる中で圧倒的に多いコメントが「なんで解けるの!?」です。
確かに算数とはいえ、当ブログで紹介している問題は算数オリンピックや難関中学入試の中でも粒ぞろいのものばかりです。数学という武器を持っている大人ですら苦労する問題もとても多いでしょう。
僕がこのような問題を解けてしまう理由はただ一つ。成功体験の積み重ねです。
算数や数学に限らず「応用問題は基礎の積み重ねだから、基礎をしっかり身につけよう」という言葉はよく耳にすると思います。自分はこれは確かに正論だと思います。応用問題はトリッキーな知識がないと解けないなんてもんだったら僕もやる気なくします。
しかしここには大前提が抜けていると思います。基礎を積み重ねたところで、どの道具をどの順番で使うべきなのかがわからなければ全てパァです。
何が言いたいかというと、「道具」を使って「課題を解決」したという成功体験が必要なのです。成功体験があるからこそ似たような状況が現れた時に「この前この方法うまくいったから今回も試してみよう」となるわけです。
そのような小さな成功体験を積み重ねまくれば目の前の課題に対して初手から様々な「道具」の活用を思いつくのです。
ここで、2016年のジュニア算数オリンピックで出題された問題を見てみましょう。
【問題】
図のような正10角形の内部に長方形がある。長方形の面積が100㎠の時、正10角形の面積は?

【解説】
多くの人は特に何も考えず下のような補助線を引くことを考えたと思います。なんでかというと、
- 正多角形は対角線て分割すると合同な二等辺三角形に分割される
という事実を使って何かしら問題を解いたことがあるからです。「分割したら綺麗な状況になる」ということを知っているだけでもこの初手は思いつくかもしれませんが。

その中から長方形をぶった切ってる2本の対角線に着目します。なぜなら
- 長方形の対角線はそれぞれの中点で交わる
という事実を利用して問題を解いたことがあるからです。これに関しては不要な対角線を省くプロセスが入るので、長方形の性質を知っているだけではこの手は選択できません。無意識のうちに「長方形は対角線に注目するといいことがあった」という経験に基づいて手段を選択しています。

すると、長方形は対角線によって面積が等しい4つの領域に分割されます。案の定ここでも長方形の対角線が役に立ったわけです。

あとは正多角形の性質を使って、上の黄色の三角形を10倍してしまえばおしまいです。またしても正多角形を分割して成功を収めました。
この算数オリンピックの問題は難問とは言えないかもしれません。でも「対角線による分割が役立った」という教科書レベルの知識によって導かれた成功体験が次に正多角形の問題を扱う時に効果を発揮します。
現に、自分も下の記事のような難問を解く時にもそういった成功体験からくる経験則が役に立っています。
教科書レベルの基礎を覚えるだけでなく、その基礎レベルの問題を自分で解決したという成功体験がセットになって「基礎が身についた」と言えるでしょう
この話は算数に限った話ではありません。プログラミングでもサンプルコードの丸パクリの繰り返しで勝手をつかんだり、仕事でも「このフレームワークが解決につながったから次も試す」。研究でも「この人の論文は参考になったから今後も参考にしよう」なんてことはよくある話です。
大きいことを成す前に小さな成功体験を大事にしていきましょう。
2013年 算数オリンピック ファイナル
こんにちはお久しぶりです。
2,3日更新が滞ってしまい、その間に当ブログに訪問してくださった方すみませんでした。
今日は朝霞訓練場で行われた「自衛隊観閲式 総合予行」の観覧に招待してもらいました。自衛隊の観閲式とは、基地や隊の創立・創隊記念の式典で、国民に自衛隊への活動の理解や周辺国への牽制のためにに執り行われるようです。
自分はそんなことは全然知りませんでしたが、各隊・車両の行進(初お披露目のF-35戦闘機の飛行もみることができました!)や、装備品(戦車などの車両)の展示、隊員有志による音楽演奏などを見れてとても楽しかったです。しかも、詳しい友人とともに観覧したので色々知識もついて一石二鳥でした。




では、今日の問題がこちらです。
2013年の算数オリンピック ファイナルから少しトリッキーな面積の問題を抜粋しました。今回の図はとても簡単なので、問題文を読んで自分で図を描くところからスタートしましょう!
【問題】難易度:★★★★☆
三角形ABCにおいて、AB=7cm、角B=22.5°、角C=45°のとき、
三角形ABCの面積は?
【解説】↓
続きを読む2005年 算数オリンピック ファイナル
こんにちは。
昨日の書評はいかがでしたでしょうか?
普段感想文や論評を書くことはないのでかなり手こずりましたが、今後もちょいちょいこういう記事を入れていこうと思います。文章力の向上に期待していてください・・・!
さて、本日は昨日の記事の最後に問題を乗せていたことにお気づきでしょうか?
え?気づかなかった。という人のために問題も再掲しておきます。
そして気づいていた皆様、お待たせしました。今回は解説付きです。
2005年の算数オリンピック ファイナルからの抜粋で、実際の問題とは少し改題してあります。チャレンジした人はわかると思いますが、かなりの難問だと思います。
【問題】難易度:★★★★★
図のような台形ABCDと台形EFGHの面積の比を求めてください。
ただし、AB=AD=EH、BC=EF=GHです。
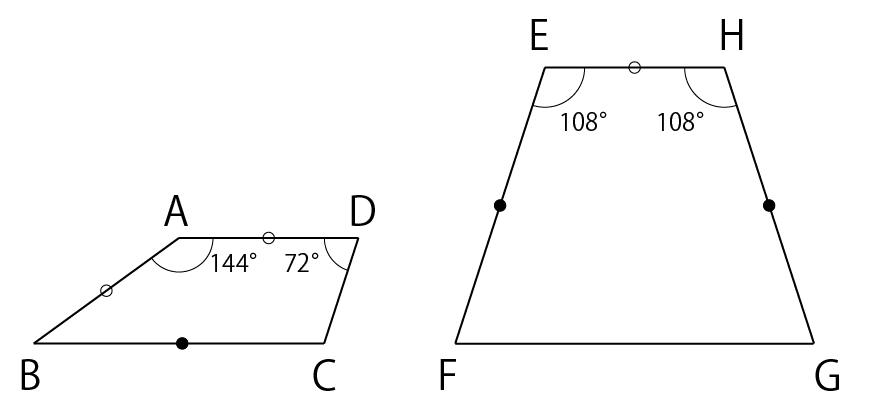
【解説】↓
続きを読む