2006年 算数オリンピック トライアル

こんにちは。

台風21号の影響で飛行機飛ばないんじゃないかと危惧しています。管理人です。

夏休み最大のイベントなのでなんとか決行したい・・・！

前置きはこれくらいにして、早速本題に入りましょう。

今回持って来た問題は気づけばシンプル。つまりこれまでどれだけ図形と親しんで来たかが問われます。

図形と親しんだと言っても、超難問に対して百戦錬磨になる。ということではなくて、普通の教科書レベルの図形問題（有名三角形や正多角形レベル）に親しむ。といった程度で十分です。

それってどういうこと？かと言うとシンプルに言えば、図形の性質や出てくる数値をどれだけ注意深く見て来たか？と言うことです。

問題はあえて文章で書きますので、図を描くところからぜひチャレンジして見てください（と言ってもサムネに図が出てしまっていますがそこはご愛嬌）。

【問題】難易度：★★★★☆

へこみのない四角形ABCDは以下の条件を満たしている。AB＝BC＝CD、角ABC＝168°、角BCD＝108°である。この時角CDAの角度は？

※へこみのない四角形とはいわゆるブーメランみたいな形になってないよって意味です。

【解説】↓

YouTubeにシンプルな解説を載せてみました。（2020/08/24）

詳しい解説はいらないや！という方はこちらをご覧ください。

【美しい！】算数オリンピック 2006年 トライアル 【角度の良問】

いつも通りステップごとに見ていきましょう。

まずは"【鉄則その１・図は自分で描く】"。

168°や108°や”凹んでない”などやや見慣れない設定に困惑した方も多いと思います。

AB＝BC＝CDを再現することはさほど難しくないですよね。角度を再現する簡単なコツは有名で描きやすい角度から逆算することです。

本問であれば、

108°は120°と90°の間で、どちらかといえば120°寄りかな。とか、168°は150°と180°の間で、どちらかといえば180°寄り。のような感じです。

120°や150°もそれぞれ180°から60°や30°を引けばいい感じに作れると思います！ここは訓練ですね。

条件を全てクリアした図は以下のようになります。

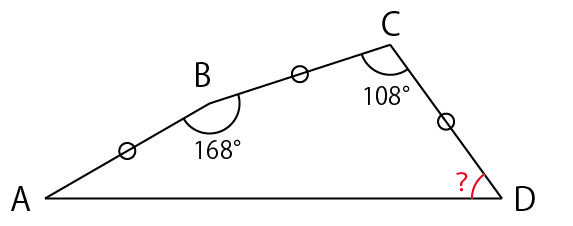
なかなかイビツな四角形ですね。そもそも四角形の角度のうち二つしかわかってない（逆にいえば２つわからないところがある）のに片方特定できるの？って疑問が湧きますね。非常にうまく作られている四角形なんだなと予想がつきます。

それでは"【鉄則その２・数値を書き入れる】"の番。

といきたいところですが、こういう意味深な問題にありがちなのが、初期状態のままでは読み取れる情報（問題を解くヒントになる情報）がぱっと見すぐ出てこない・書き足せないと言ったことが多々あります。

そのため今回はあえなくこのフェーズからは一度撤退。

気を取り直して”【鉄則その３・関連性を探る】”のフェーズ。

問題こなれてきた人や、このブログの読者の中にはいろんな"関連性"が見えている人も多いと思います。

例えば二等辺三角形を作るべく、AとCを結んだり、BとDを結んだり。しかし、見慣れない角度（6°）を新しく作ってしまったり、２つの角度がわからない三角形ABDなんかを作り出してしまい迷宮入りです。

次に、等辺があるなら上手くくっつけれないか？という考えも浮かびます。しかし、今回は与えられた角度だけで90°や180°のような角度を作れないことにすぐ気づくでしょう。

上の方法は本問では残念ながら有効に働きませんが、こういうアプローチが図形を見る目を育んでいきます。

ではどうするか。次は角度の関連性に注目して見ましょう。すぐには見抜けない人もいるかもしれませんが、108°は正５角形の１つの角度、168°は 正30角形の１つの角度であることが読み取れます。これらの図形と絡めて考えて見ましょう。

しかし、正30角形は上手く描くことが困難ですし、私も（皆さんも）できれば描くチャレンジはしたくないでしょう。なのでまずは簡便な正五角形から攻めて見ることにしましょう。

時にはこういう横着も大事です。これでダメなら正30角形で攻めれば良いのです。

問題の図に正五角形を無理やりつけると下の図のようになります。

168°は60°と108°に分かれますね。

正五角形（に限らず正多角形）を作ると何が嬉しいかというと、等辺がたくさん増えることです。

下の図は上の図となんら変わりがありませんが、着目する等辺を変えました。

BA＝BFと、この２辺で挟まれた60°に着目すればこれはもうヒントはいらないでしょう。正三角形が隠れていることに気づきます！

するとどうでしょうか。下の図のように辺ADを境にして、四角形ABCDと四角形AFEDが上下反転の関係にあることに気づけましたでしょうか？

ここまできたらゴールは目前です。上下反転ということは”同じ形”なので角CDA＝角EDAです。

つまり角CDAは角EDC＝108°の半分で、角CDA＝54°となります。

いかがですか？毎度のごとく長々と説明しましたが、正五角形に気づけば瞬殺ですよね。これを見抜くには訓練が必要ですが、特別な知識は必要としませんよね。

つまり、教科書レベルの図形と親しんでいればこの問題は解けるのです。

そして、ステップごとに分けて考え、これらのステップを繰り返すことも大事です。

つまり、図形問題は「ステップとその繰り返し」という根幹に、「図形と親しんだ経験」という養分を与えることによって解答という「木」が完成します。

では今回はこの辺で。お疲れ様でした。