2018年 ジュニア算数オリンピック ファイナル 【その1】
こんにちは。
当ブログでは灘中学をはじめとする難関中学入試や、算数オリンピックを中心に「思考体力」が鍛えられそうな図形問題を中心に扱っています。
図形力は幼少期の教育に大きく依存するという説もあるようですが、僕は何歳からでもいいと思ってます。
確かに解法が確立されてないような初見の難問・奇問はそういう力に依存するのかもしれません。しかし、そういう”型破り”の問題を処理するためにはまずは”型”を身につける必要があります。(型破りは型の派生だったりします。)
このブログを通して、その”型”を少しでも身につけてもらえたら嬉しいです。図形力は入試や算数オリンピックに役立つことはもちろんですが、日常のことにも役立ちます。
わかりやすい例で言えば地図を読み、どの経路がベストなのかを考えたりなどです。
「なんだその程度のことか」と思われるかもしれませんが、意外とこれできない人は多いです。
今回は少し型破りな奇抜(しかしエレガント)な解法をご紹介したいと思います。もっとシンプルでわかりやすい解説は【その2】でやろうと思います。しばしお付き合い願います。
図形も描きやすい問題なのでチャレンジしてみてください。
【問題】難易度:★★★★☆
台形ABCDについて次のような情報がわかっている。
AB=AD、BC=5 cm、角A=角B=90°、角C=30°
このとき台形ABCDの面積は?
【解説】↓
YouTubeに簡易版の解説を載せてみました。(2020/08/11)
詳しい解説はいらないや!という方はこちらをご覧ください。
【柔軟な発想で!】Jr.算数オリンピック 2018年 ファイナル
今回は冒頭でも述べたように少し奇抜な解法で解説を進めます。
みなさん下の図のような台形が描けていれば"スタートライン"はクリアです。
(それにしても面積出したいのに長さ一つしかわかってないなんて・・・)

ここからいろいろ情報を探っていきましょう。
こんな図形見せられたら正方形と三角定規(正三角形の半分)に分割したくなりますね。本能に従いましょう。

すると、辺の長さの関係が下のように得られます。中学数学であれば?の比も表せますが今回は算数なので今回はご法度(中学数学使うとこの問題は瞬殺です)
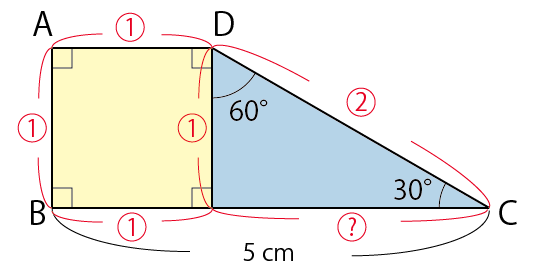
正方形が絡む問題は「別の正方形」をどこかに作り出して、わかってる長さを利用する。という手法をとりたくなります。(取りたくない人も今回はとってください)
わかってる長さはBC=5 cm だけなので、一辺が5 cmの正方形を作りたいなと考えます。(これは経験からくるカンってやつです)
ここで下の赤枠の図形のように変形させることにしましょう。この図形は台形ABCDと同じ面積であることをお忘れなく。

で、こいつを4個寄せ集めるとめでたいことに一辺が5 cmの正方形が姿を現します。

ここまできたらゴールは目前。正方形の面積の1/4なので、
(台形ABCDの面積)=5 × 5 ÷ 4 = 6.25 (㎠) となります。
パズルのように綺麗に解区となんかすごいことやってるように見えて僕は好きです。しかしこの問題こんな仰々しいことしなくても解けます。
いつもの型に従っての解説は【その2】でやりますのでお待ちください。
SNSなどでシェアしていただけると励みになります!
では今回はここらで失礼します。