2007年 算数オリンピック ファイナル

こんにちは。

昨晩は大学1.2年の頃の友人たちとかなり久しぶりに飲んできました。それぞれ専攻もキャンパスも進路も違ってまともに会うのは3,4年ぶりでした。当時の話で盛り上がり、若返ったような気分で楽しかったです。

あった友人にもブログ見たよと言ってもらえたり、その他いろんな場面で「わかりやすい」「面白い」などの反響をいただけるようになってきてとても励みになります。ありがとうございます。

さて、今回は久しぶりに角度の問題です。算数オリンピックの角度の問題もある程度解き方が見えてきてしまった人もいるのではないでしょうか？

ぜひ正解目指して解いて見てください。

【問題】難易度：★★★★☆

図の？の角度は何度でしょう

【解説】↓

YouTubeに簡易版の解説を載せてみました。（2020/07/18）

詳しい解説はいらないや！という方はこちらをご覧ください。

【簡単そう？】算数オリンピック 2007年 ファイナルの良問！

 ではいつも通り段階ごとに見ていきましょう。

角度の問題だと割と”【鉄則その１・図は自分で描く】”と”【鉄則その２・数値を書き入れる】”を同時に考えていくと特徴を捉えながら問題を眺めることができるかなと思います。

まずは適当に書いて、分かる情報を書き込んで、性質を発見して図を修正するイメージです。

そのままの図で分かる情報を書き出すと下の図のように角度と等辺が見つけられます。

三角形の内角の和が180°であるということしか使っていないので難しいこともありませんね。今後の説明のために頂点には記号をつけておきます。

では次は"【鉄則その３・関連性を探る】"のフェーズ。

上の図では３本の等辺の位置関係がバラバラでどうやって問題に活かせば良いのかわかりづらいです。こういう時はどうにか（くっつけたり折り返したり回転させたり・・・）して等辺を増やす方策が有効です

そしてわかっている角度は全て20°刻み。1995年 算数オリンピック ファイナルの記事でも紹介しましたが、角度を足したり引いたり何倍かしたりして有名角を作り出すことが有効です。

これらのことを考慮すると、有名角である60°（＝80°ー20°＝40° + 20°＝20°×3）を用いて、等辺を増やすために正三角形を作ることにしましょう！

作り方は様々ですが、もともとある辺を一辺に持ち、かつ80°ー20°＝40° + 20°を使える作り方は下図のようになります。

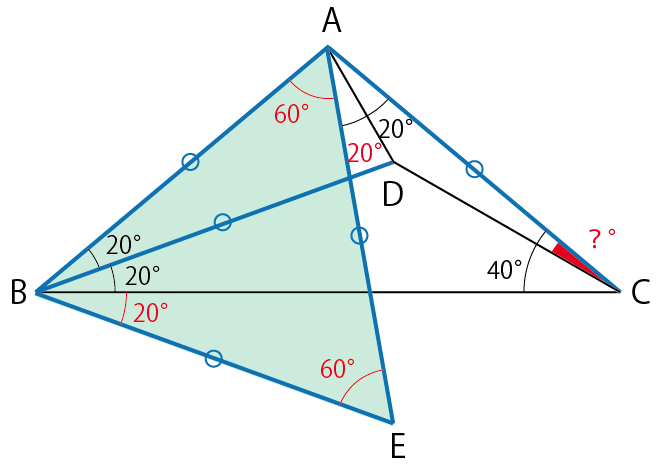
ここで、新しく作られた等辺からAE＝ACと角EAD＝角CADに着目すると、三角形EAD＝三角形CADがわかります。つまり、？を移動させることができました。

図形の難問ではこのように「合同な図形を使って角度をわかりやすい位置に移動させる」という技がよく使われます。

ここまで分かればゴールは近いです。BD＝BEより、三角形BDEが二等辺三角形になっていることがわかります。したがって、下の図のように角BED＝70°です。

よって、？＝10°と求められます。

算数オリンピックではやたらと正三角形が隠れていることが多いです。それだけ神秘的な図形ということなんでしょうね。

それでは今日はここでおしまい。「この問題解いてほしい」というリクエストもお待ちしております。